There are a number of questions our Maths Specialists see crop up again and again, ranging from simple tricks like finding the x and y intercepts of an equation, to more advanced concepts like solving quadratic inequalities. So we thought it would be helpful to share these with you, along with tips on how to find the solutions.
One of our expert Maths Specialists, Jemma, shares the top five questions she sees, the most common issues and mistakes students make, and her tips on how you can work around them.
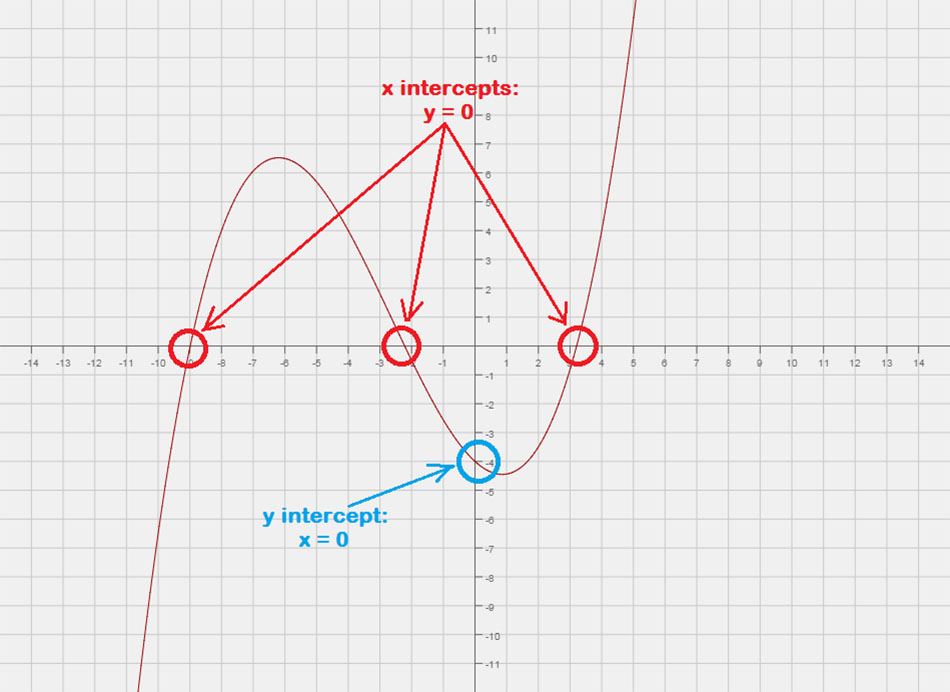
1. Finding x and y intercepts of an equation
It’s easy to identify the x and y intercepts on a graph, but students frequently struggle to find them using only the equation. However, it just requires a simple trick:
-
To find the x intercept(s) of an equation, substitute in y = 0 and solve for x.
- To find the y intercept(s) of an equation, substitute in x = 0 and solve for y.
2. Finding compound interest
Most students are familiar with using the formula A = P(1+r)t formula to calculate compound interest when it is compounded annually (once a year). However, many have difficulty when the interest is compounded more frequently. In this case, we can use a slightly different compound interest formula (shown below) to account for the change in compounding period.
-
If interest is compounded monthly, then n = 12
-
If interest is compounded daily, then n = 365
Once n has been worked out, this formula can be used in exactly the same way as A = P(1+r)t.
3. Finding the equation of a parabola
In this frequently asked question, students are given the coordinates of three points and asked to find the equation of the parabola passing through those points. The following steps should be taken to solve this type of question:
-
Write down the general equation of a parabola
y = ax2 + bx + c
-
Substitute in each set of coordinates, one at a time, to get three simultaneous equations.
For example, if the parabola passes through (3,4), the first equation would be:
4 = a(3)2 + b(3) + c
4 = 6a + 3b + c
-
Solve these three equations simultaneously to find values for a, b and c.
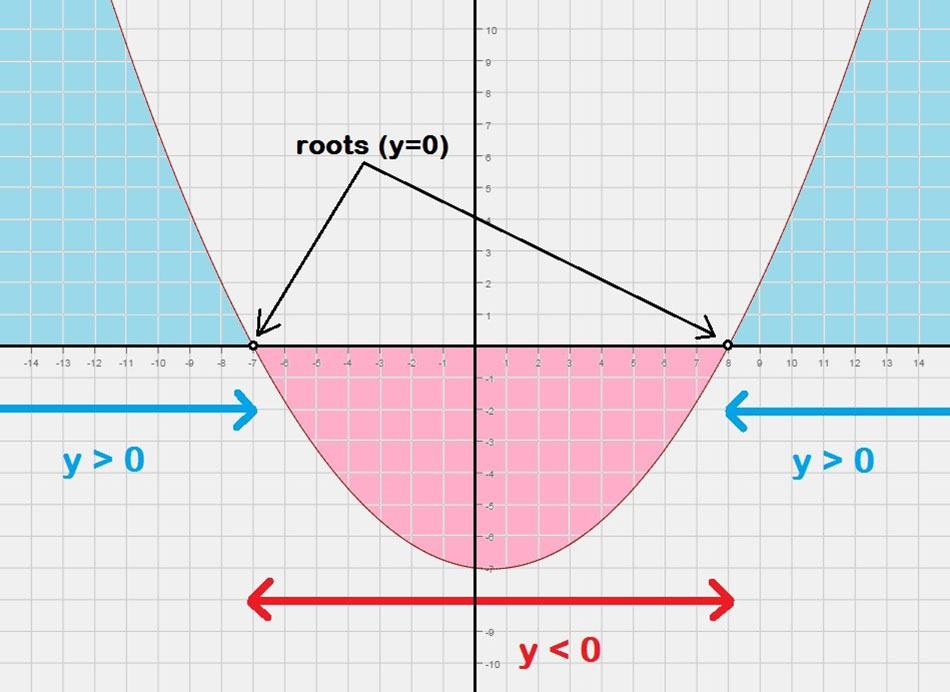
4. Solving quadratic inequalities
I frequently encounter students who have not been taught how to solve quadratic inequalities, but are still expected to apply this concept in questions. Here are my tips on how to approach this:
Solving a quadratic inequality is very much like solving a quadratic equation.
When solving equations, we try to find roots (like the ones marked “y = 0”). However, when we solve inequalities, we try to find intervals, such as the one marked “y > 0”.
We can follow the following steps to solve a quadratic inequality:
-
Solve the inequality as though it were an equation to find the roots, which become the boundary points for each interval.
-
These roots will be part of the final solution if the original inequality includes equality (i.e. y ≤ 0 or y ≥ 0).
-
In between the “y = 0” points are intervals that are either:
-
Greater than zero (“y > 0”), or
-
Less than zero (“y < 0”)
-
Select points from each of the intervals. Substitute each of these test points into the original inequality.
-
If a test point satisfies the original inequality, then the interval that contains that test point is part of the solution.
- Represent the final solution in either inequality form or interval notation.
5. Checking your solutions
From Year 3 through to university, one of the most important steps of solving a maths problem is to check your solutions. There are several ways that you can check solutions, but the key ones are:
Check to see if your answer makes sense
This is our “common sense” test, where we can weed out any solutions that are obviously wrong.
-
For example, let’s say we get a solution of 100 kph.
-
If the question was to find the speed of a car on the open road, then this is a reasonable answer – it makes sense.
-
However, if the question asked us to find the speed of a marathon runner, then this answer is not reasonable – the marathon runner would need to run twice as fast as Usain Bolt! Therefore, we can eliminate this solution.
Substitute your answer back into the original equation to see if it works
Here we check to make sure that a solution is correct by making sure that it satisfies any and all equations and/or inequalities in a problem.
-
For example, we get a solution of x = 4 for the equation 2x – 7 = 1
-
We substitute x = 4 into the equation to give:
-
2(4) – 7 = 1
-
8 – 7 = 1
-
1 = 1
-
Since our answer worked, the check passed, and x=4 is a correct solution.
If you liked this, you might also be interested in 'What every student should do in the last 10 minutes of a maths exam'.
If you're ever stuck on a maths problem or need help understanding a concept, connect with one of our expert online Maths Specialists who are here to help in all maths subjects.
